The Wallis Product

 

 

 

 

 

 

 

 

 

Brian Morton

Reading Classics

May 22, 2003

 

 

 

 

 

 

 

 

            John Wallis was born in 1616 in Ashford, England. In 1630, Wallis considered himself ready for the university at the age of 13; however he went to Martin Holbeach's school in Felsted, Essex. Most of the best schools of the time did not consider mathematics important, so he did not get exposure to math until his brother showed him the rules of arithmetic. This sparked his curiosity and eventually led him to work on mathematics. During the time Wallis was studying math, the state in which math was in was brimming with potential. The subject of Infinitesimal was one of profound study in the beginning of the 1600’s. Kepler not much later conceived the circle as being made up of an infinite number of triangles having a common vertex at the center and having infinitely small bases. This helped familiarize the notions of infinitely great and infinitely small. Cavalieri, a mathematician that Wallis himself was interested in, was attracted to Kepler’s work and put forth the notion that a line was made up of an infinite number of points and a surface was made up of an infinite number of lines and a surface was made up of an infinite number of surfaces. He made it an axiom that “any magnitude may be divided into an infinite number of small parts which could be made to bear any ratio one to another” (26). This is the state of mathematics when Wallis comes to pursue its knowledge. In Arithmetica Infinitorum, Wallis comes very close to finding the quadrature of the circle.

            He starts off using the fact that the volume of the cone is one-third the volume of the circumscribing cylinder, a fact know since Archimedes. He says that the radii of the circles in the cone increase in an arithmetic progression so the area of the circles increases in a duplicate, meaning squaring. This leads us to the ratio of:

 

            He then goes to that if we take the triangle gotten from intersecting the cone with a plane and consider the rectangle gotten the same way from the cylinder we know the ratio of the areas is one-half so we get a new ratio.

Wallis does the same for the parabola and the sphere getting new ratios of different sums one involving square roots and the other with the difference of squares. He considers lines perpendicular to a diameter starting from a radius and working down to a line segment of length zero, he says that these lines form a series in a progression.

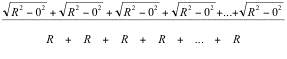Therefore, he concludes that if he can find the ratio

we have found the ratio of the quarter circle to the square with the radius as the side, in other ward the quadrature of the circle,.

In order to do this he first looks at the quadrature of the equations of and concludes that the area under the curve has a ratio of to the area of the unit square. He proves this by considering the ratio of is by an inductive argument, which he calls the Method of Induction. This method is the precursor to the Mathematical Induction of today and is not quite as rigorous. For his proof of the ratio of squares it goes like this:

and generally, he concludes,

           

If we let n get large then the ratio approaches one-third, which proves his assertion from above. As we can see this method lacks the rigor needed today but it does require a certain amount of insight into patterns of numbers.

            In the ratio he wants to prove there are fractional powers so he then moves to considering what happens to the ratio of an increasing progression of terms to a fractional power to the sum of the highest term added to itself the number of terms in the sequence. In Proposition 59 he gives us a chart for powers of the form p/q. The ratio of

 

 

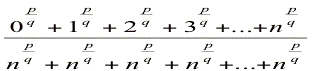
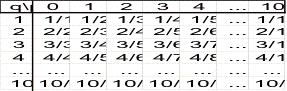In proposition 64 he states that if we take an infinite series of quantities starting at 0, continuously increase in the ratio of any power, an integer or rational fraction, then the ratio of the whole series to the series of as many numbers equal to the highest number is 1 divided by the power plus one. This is equivalent to saying for any rational number r. What is amazing is that he asserts that this is true even for irrational number such as the ratio will be 1 to + 1. He seems to be able to state this using the idea of continuity but it really is without proof.

            Since the terms in the series for the circle involve the difference of two series raised to the one-half power he first looks at the case of differences. In this study he gets proposition 111. Proposition 111. If from a series of equals are subtracted term by term by a series of the first, second, third, nth order, these difference give

of the total series of equals. In today’s terms he has calculated the integral . He then turns to a more general case of when the terms are of the form , which is equivalent to finding the integral . For this study he eventually creates a table for the values of p and n and the ratios they determine, which the ratio is one to the numbers in the table.

 

 

He is able to generate this table by noticing the fact that each entry of the table is the sum of the entry above it with the entry to the left of it. This enables him to find the ratio for any two integers. He recognizes a pattern in the numbers for each row, the entries in the pth root row are generated by the equation where n is the power. In particular he notices that the entries in the row p=2 are the Triangular numbers and those with p=3 are the Pyramidal numbers. To get the desired ratio he needs to expand this table to include the results for p = n = ½. He expands this table by adding a column in between each existing column and does the same for each of the rows. Wallis says that all of the entries with p=2 and with n= 1,2,3,… satisfy the rule

then, by his Method of Induction, why should not this rule hold for values in between these, like 3/2? He generates the new column by taking the general rule and setting n= 1/2, 3/2, 5/2, 7/2, etc. Basically he extends his equation from an equation from the integers to the integers to a function on the rationals and assumes they are the same. This seems reasonable however it is completely unjustified, for there are odd things that can be proven by misapplying mathematical induction. It is amazing that this actually works, well at least, in giving an accurate approximation to pi. With his keen ability to see patterns he is able to fill in the gaps in his table, where b is the desired ratio from the beginning or b= . Wallis actually used a box to represent pi over four. He was also
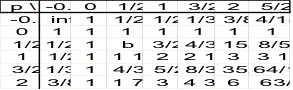the first one to the symbol for infinity.

 

He, in particular, noticed that the odd entries in the third row were given by and the even entries in the third row are given by . The rest of the rows have a similar pattern to the entries but this one is the most important since it involves the value b that he is looking for. He then takes the ratio of two consecutive odd entries and compares it to the ratio of two consecutive even entries and continues to do so and get the ratios form a decreasing series of . He also sees that in three consecutive terms, even and odd, which the middle term squared is greater than the product of the end terms. With this being the case he can easily show that

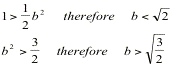
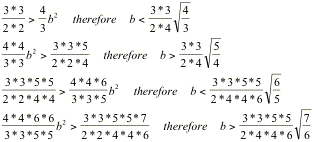
Proceeding in this manner he easily shows that b is less than

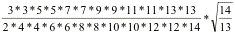
but is greater than

.

If we let the number of terms become as large as we like we can get as close an approximation to b as we want. He concludes that if n is large enough

.

Several mathematicians at the time did not believe this formula until it was shown that it contained the approximation to b already know to them.

Wallis also wrote b as

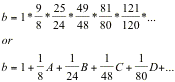
where A, B, C, etc. are the first, second, third, etc. terms in the first expression for b, A=1, B=9/8, etc.

Wallis not entirely satisfied with his expression since he did not get an absolute value but an infinite sum, he sent it to Lord Brouncker. Brouncker did not succeed in getting an absolute value but he did write an expression which started the study of continued fractions. He said that b was

continuing on until infinity.

            Through his uncanny ability to see patterns and his use of his favorite interpolation method that of induction, which seems luckily applied to his studies, he was able to get very close to the quadrature of the circle. He also made the notion of induction acceptable which it became more rigorous. By his correspondence to Lord Brouncker he also inspired too some extent the study of continued fractions.

 

 

 

 

 

 

 

 

 

Works Cited

Scott, J. F. The Mathematical Work of John Wallis D. D. FRS. 1616 – 1703

Wallis, John. Analysis Before Newton and Leibniz. Computation of pi by

            Interpolations.